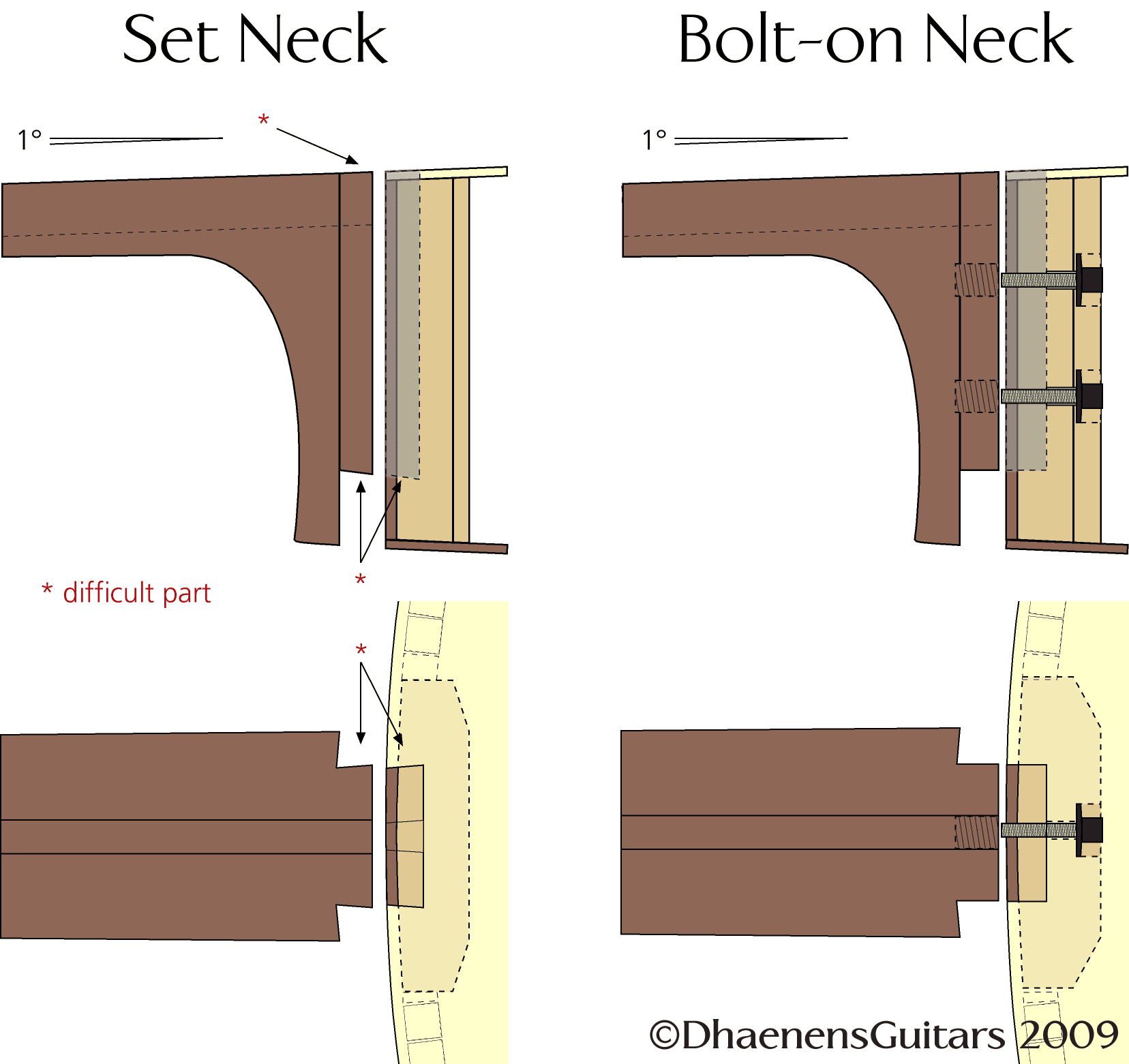
12 or 14 frets clear to the body? Or something in between?
- door Guy D'haenens
- •
- 15 aug, 2017
- •
13 would be nice
Guitar players who go out to buy a guitar hardly ever think about string length and the number of frets clear to the body. That is because there isn’t much of a choice. All the major acoustic steel string guitar building companies standardize on 25.34″ and 25.51″ and 14 frets. Once in a while, you can come across a 12 frets 0, 00 or 000 model that is sold as a “blues” guitar. And yet, the string length and the number of frets is not an axiom.
The first acoustic steel-string guitars had 12 frets from nut to body and various string lengths ranging from 23.5″ (59,7 cm) to 26.38″ (67 cm). This variation is easily explained by the fact that all those guitars were made by hand in small shops or ateliers. The Martin guitar company was one of the first to offer standardized models. One of their first models (1860-1870!) was almost an exact copy of a ‘Spanish’ guitar with 12 frets clear to the body: the 0-model. In 1877, they released a guitar with a slightly larger body, the 00. In 1902, model 000 was released and this model became the flagship of the company until the end of the roaring twenties. Tens or hundreds of each model were sold which was, taken into account that guitars were far less popular than banjos and mandolins, a very good sales figure.
In 1929, Perry Bechtel, an extremely popular and talented banjo player and guitarist, approached Martin III asking to build him a 000-model with 14 frets clear to the body so he could use the higher register of the guitar just like he was used to on his tenor banjo. He also asked for a solid peghead – also like on a banjo – and a louder sound. A couple of months and several modifications later, Bechtel received his OM (orchestra model) and started performing with it. The guitar became so rapidly popular that by 1933, the OM-model with its 14 frets became the standard model for Martin. After 1933, Martin added an ‘S’ to the names of all 12-frets guitars. ‘S’ for standard, not for the slotted peghead as many assume. In short, this is how the OM-model became the standard for all acoustic steel-string guitars. In figure 1 you can clearly see the evolution of these models. 0-28 and 00-28 both have a 24.9″ (63,9 cm) scale length while 000-28 and OM-28 have a slightly larger 25.4″ (64,36 cm) scale length.

Figure 1: Evolution of popular Martin guitars
I created a little animation to better illustrate the changes Bechtel ordered:

Figure 2: Animated view of the transition of 000-28VS to OM-28V
The first thing that you’ll probably notice in figure 1 is the increase of body size: the OM is huge compared to model 0. And what you can’t see is that the body depth is also increased in order to get a ‘bigger’ sound. But if you have ever played on a 00-model, you will agree with me that a OM-model, although louder, has a more compressed sound than a 00-model. It’s like there’s something missing. Warmth, depth, sensitivity.
And this started me thinking. Although the 0-models have a larger air-chamber above the soundhole (and note that the area of the top plate above the soundhole is quite rigid and doesn’t flex), that loss on a OM-model is compensated by the increase in body size and body depth. So the only other thing I could think of was the position of the bridge.
Now take a closer look at the position of the bridges of the models in figure 1. On a 0-28, the bridge is positioned almost at the same spot as on a spanish guitar; on later models there is more and more belly below the bridge.
In my previous articles, I have already explained the function of the top plate: it is a membrane that is set into a pulsing motion by the movements of the strings. The strings are attached to the bridge and the bridge acts as a hinge on the top plate. In order to get a maximum transfer of the movement of the strings to the top plate, the relative position of the bridge is extremely important. By increasing the body size over the years, this position became less optimal. So, in order to get that special 00-sound on a OM-model, the position of the bridge must be lowered, away from the soundhole. This could be done by increasing the scale length, say to 26.4″ or longer. But then only guitarists with huge hands would be able to tame a beast like that. An other option would be to move the neck downwards. After a few experiments, I came to the conclusion that by fitting the neck at the 13th fret, the bridge could be positioned right on the optimum spot.

Figure 3: Difference between a OM-model with 13 and 14 frets clear to the body
I made a such a guitar (an Archback Fingerstyle Artist model with Spanish spruce top, French walnut B&S and neck) several years ago, and IMO it sounded just great and as I expected it to sound. The highs were crisp and vibrant while the mids and basses were deep with lots of character. But (isn’t there always a but?) I noticed that guitarists – even veterans – who tried this guitar out got pretty much confused when playing the upper register. The long stored visual link between finger position and sound didn’t match up any more. The human brain is a funny thing, isn’t it?
That guitar is no longer among us. As everybody liked the sound but was reluctant to buy the guitar, I dismantled it and revamped it into a 14 frets model. And I still regret it.
Now, I’m building a new one in Kotibe with a cutaway. Hopefully, that cutaway will help in restoring the visual link.
Guy's Blog
Guitars are designed for the 12-tone equal tempered tuning (12-TET). In a 12-tone equal tempered tuning, an octave is divided in 12 semitones at an equidistance of each other: C, C# or Db, D, D# or Eb, E, F, F# or Gb, G, G# or Ab, A, A# or Bb, B.
12-tone equal tempered tuning assumes that e.g. C# is soundwise exactly in the middle of C and D. As you could have guessed, in real life it’s not, it’s only in the mathematical middle and soudwise a bit on the sharp side.
Guitars and all other instruments are tuned at A4= 440 Hz. In 1939 musicians world-wide came to a consensus on that pitch. Before that time, the pitch had been 435 Hz, 374 Hz (1648) and 503 Hz (1361) but those were merely guidelines. Each maestro was free to compose or direct at a lower or higher pitch.
(Hz is the unit to express the number of oscillations of pressure in a sound wave. 440Hz means that there are 440 oscillations per second.)
When you pull an unfretted A-string on a tuned guitar, you’ll hear 110 Hz. When you fret that string at the 12th fret, you’ll hear 220 Hz. That’s exactly the double. Double or half the Hz of any tone is called an octave. Fret that string at the 24th fret and you’ll hear 440 Hz, again one octave higher or 2 octaves higher than the tone of the unfretted string. What you have done each time, is shorten the string by half. A shorter string vibrates at a higher speed thus producing more oscillations per second. A string at 440 Hz oscillates twice as fast as a string of double that length.
The guitar is fretted so we can easily pick the correct notes. Those frets are laid out according to a simple calculation.
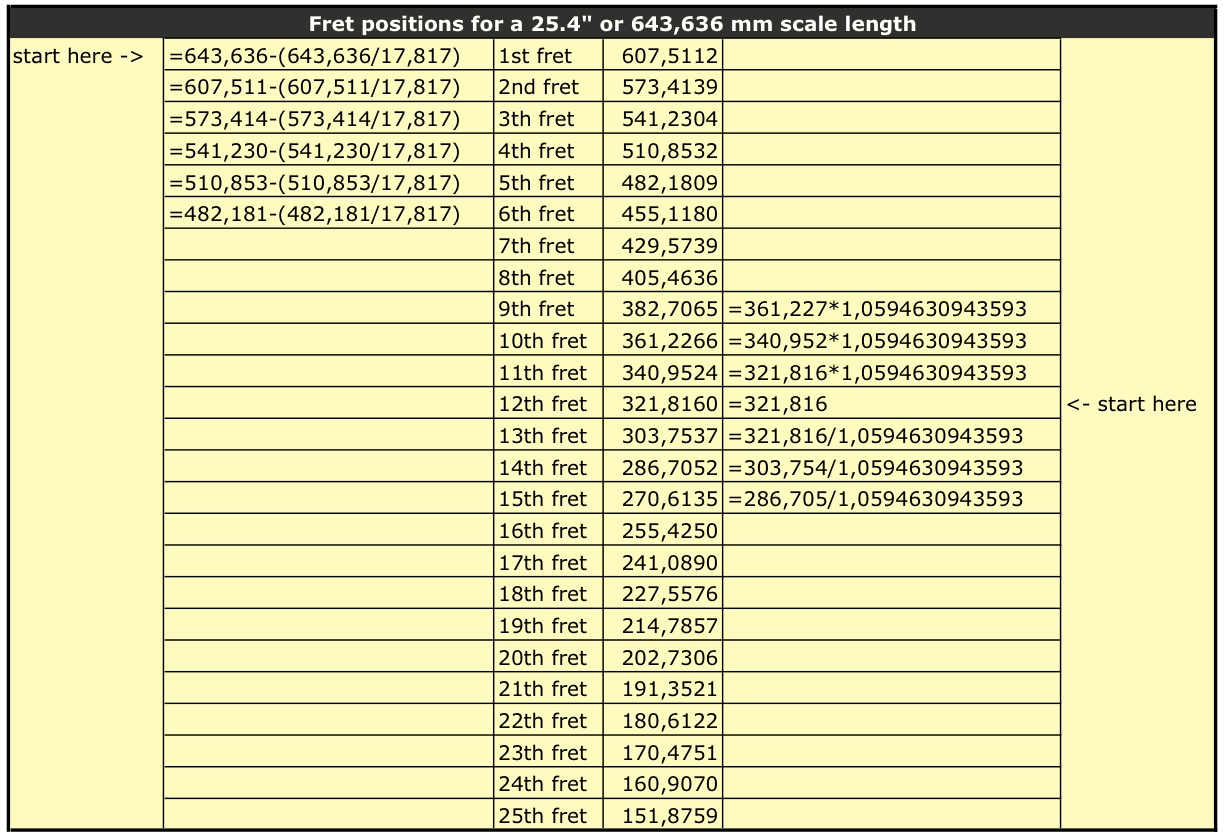
Assume that the scale length of your guitar is 25.4″ (actually it’s 25,34″) or 643,636 mm. The scale length is the distance between the nut and the top of the saddle. The 12th fret will be exactly at 12.7″ (25.4″/2) or 321,818 mm. And since an octave in a 12-TET scale is divided in 12 semitones at equidistance of each other, the math should be fairly simple, no? Alas, dividing 12.7″ by 12 won’t do. That is because we can’t use the distance as input for our calculations, we have to use the frequences. In a 12-TET scale, the ratio of frequencies between two adjacent semitones is the twelfth root of two. And the twelfth root of two is 1.0594630943593.
So starting from the 12th fret, the exact position of the other frets is easily calculated by multiplying or dividing the position of a (previous) fret with 1.0594630943593.
The position of the 11th fret is 340,9543 mm (321,818 * 1,0594630943593); the position of the 10th fret is 361,2626 mm (340,954294100521 * 1,0594630943593); that of the 13th fret is 303,7557 mm (321,818 / 1,0594630943593) and so on.
Another way to determine the fret positions is by using the constant 17.817. The scale length divided by this value gives us the distance from the nut to the first fret.
The following table will make it more clear: