A guitar always plays out of tune - part 1
- door Guy D'haenens
- •
- 12 aug, 2017
- •
Guitars are designed for the 12-tone equal tempered tuning (12-TET). In a 12-tone equal tempered tuning, an octave is divided in 12 semitones at an equidistance of each other: C, C# or Db, D, D# or Eb, E, F, F# or Gb, G, G# or Ab, A, A# or Bb, B.
12-tone equal tempered tuning assumes that e.g. C# is soundwise exactly in the middle of C and D. As you could have guessed, in real life it’s not, it’s only in the mathematical middle and soudwise a bit on the sharp side.
Guitars and all other instruments are tuned at A4= 440 Hz. In 1939 musicians world-wide came to a consensus on that pitch. Before that time, the pitch had been 435 Hz, 374 Hz (1648) and 503 Hz (1361) but those were merely guidelines. Each maestro was free to compose or direct at a lower or higher pitch.
(Hz is the unit to express the number of oscillations of pressure in a sound wave. 440Hz means that there are 440 oscillations per second.)
When you pull an unfretted A-string on a tuned guitar, you’ll hear 110 Hz. When you fret that string at the 12th fret, you’ll hear 220 Hz. That’s exactly the double. Double or half the Hz of any tone is called an octave. Fret that string at the 24th fret and you’ll hear 440 Hz, again one octave higher or 2 octaves higher than the tone of the unfretted string. What you have done each time, is shorten the string by half. A shorter string vibrates at a higher speed thus producing more oscillations per second. A string at 440 Hz oscillates twice as fast as a string of double that length.
The guitar is fretted so we can easily pick the correct notes. Those frets are laid out according to a simple calculation.
Assume that the scale length of your guitar is 25.4″ (actually it’s 25,34″) or 643,636 mm. The scale length is the distance between the nut and the top of the saddle. The 12th fret will be exactly at 12.7″ (25.4″/2) or 321,818 mm. And since an octave in a 12-TET scale is divided in 12 semitones at equidistance of each other, the math should be fairly simple, no? Alas, dividing 12.7″ by 12 won’t do. That is because we can’t use the distance as input for our calculations, we have to use the frequences. In a 12-TET scale, the ratio of frequencies between two adjacent semitones is the twelfth root of two. And the twelfth root of two is 1.0594630943593.
So starting from the 12th fret, the exact position of the other frets is easily calculated by multiplying or dividing the position of a (previous) fret with 1.0594630943593.
The position of the 11th fret is 340,9543 mm (321,818 * 1,0594630943593); the position of the 10th fret is 361,2626 mm (340,954294100521 * 1,0594630943593); that of the 13th fret is 303,7557 mm (321,818 / 1,0594630943593) and so on.
Another way to determine the fret positions is by using the constant 17.817. The scale length divided by this value gives us the distance from the nut to the first fret.
The following table will make it more clear:
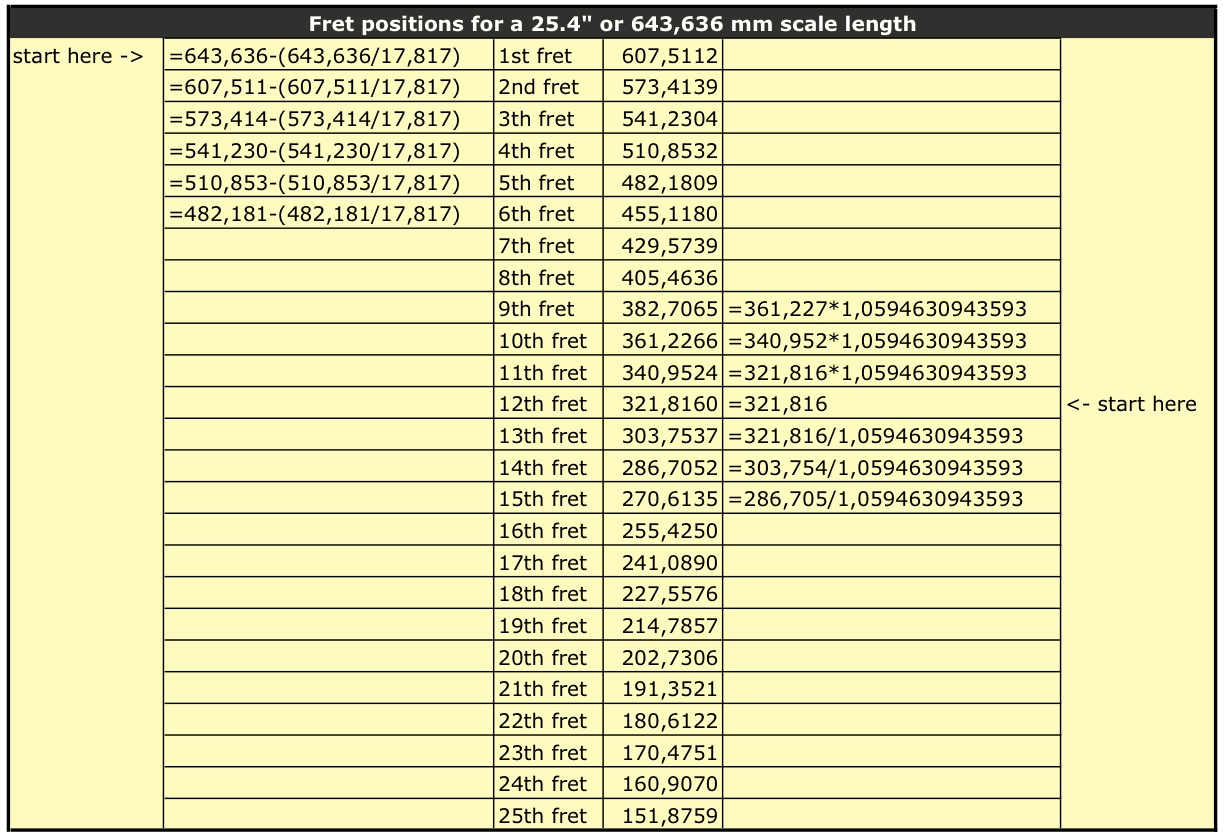
The calculation of the fret positions
Theoretically, with an exact string length of 25.4″, all frets placed at the exact positions and the open strings tuned, the guitar should play in tune. But it won’t. That’s because by fretting (pressing the string down), the string is stretched and the pitch rises. To compensate for that, the saddle for a high E has to be moved away from the nut by about 1/16″ or 1,59 mm. Heavier/thicker/stiffer strings need more compensation so the saddle for the low E has to be moved farther away from the nut with an extra 3/32″ or 2,38 mm, totalling the compensation to 5/32″ or 3,97 mm. Note that for wound strings (G, D, A and low E), it is the core that makes a string stiffer, not the windings. That’s why a saddle on an acoustic steel-string guitar is slanted/ramped.
Electric guitars have saddles with individual saddle slots. Each slot can be moved forward or backward by the turn of a screw. That is very, very handy. In fact, it is so handy that at one time Gibson decided to put that type of saddle on their acoustic guitars. Unfortunately, the weight and the mass of the saddle appeared to be a real sound killer.
This is the standard compensation technique for mass-production guitars with a 25.4″ scale length. Some of those guitars will be just fine, most of them not. That ‘general’ rule only applies to guitars with a specific string gauge and type of strings and a perfect action. A perfect action (the distance between the string and the fretboard) is only achieved when the angle of the neck to the guitar, the amount of ‘belly’ or arch of the guitar top and the height of the saddle are absolutely spot on. Changes in relative humidity will change the action and the belly of the guitar (see my previous article) and change the overall length of the strings thus ruining the intonation.
You can check the intonation of your guitar using an electronic tuner. For each string, the frequency of the 12th fret harmonic and the string fretted at the 12th fret should be the exact double (octave) of the open string. If your guitar has a ‘standard’ slanted saddle and a standard set of strings, only the metering of the high E, D, A and low E strings will be correct. The B and G strings will give slightly off readings. The reason for this is that the B string is made of heavier steel and needs almost as much compensation as the D string. The G string on the other hand has a core of thin steel wire and needs only slightly more compensation than the high E string. Some guitars have a notched saddle for the B string to get a correct intonation for that string. Some other guitars have a split saddle: a short, very slanted saddle for the high E and B and a large, slanted one laid out according to the compensation technique explained earlier for the other strings.
I generally use a wide saddle to have enough body for proper compensation. In some cases, when a customer requires a specific action and a certain type of strings, I use the hardest and toughest ebony I can find instead of unbleached bone. Ebony has the advantage that it lets an overly wide saddle ‘blend in’ with the bridge.
Although lower tension doesn’t always imply less stiffness, strings with ‘equal tension’ like the ones offered by Newtone Strings, hardly need compensation for the middle and bass strings. This means that you can’t simply swap regular strings for equal tension strings; the saddle and in some cases the bridge will have to be adjusted. On the other hand, swapping strings of gauge 12 for a set of gauge 9 will require also a saddle adjustment.
As said, changes in relative humidity can ruin the effects of a well compensating saddle. The moment the action changes, the length of the strings also changes. In order to deal with that, I use a back-slanted saddle on my guitars. Noblesse oblige to say that I didn’t come up with this idea. I picked it up on the internet from a Petros guitar but other luthiers too are using this technique. Whoever came up with this idea, it’s good thinking.
If you want to correct the intonation of your guitar, here’s a checklist:
More compensation is needed in the following cases:
- high action
- shorter scale length
- lower tuned guitar
- stiffer strings
For each string, the saddle needs more compensation if the fretted note (at the 12 fret) is sharp relative to the open string and the 12th fret harmonic and needs less compensation if the fretted note is flat. If the fretted note has exactly the same frequency as the 12th fret harmonic and has the exact double frequency of the open string, the compensation is correct.
With this, your guitar has a more or less correct intonation. I say ‘more or less’ because apart from the open string and its octave, all other notes still will be slightly out of tune.
Next time, I’ll discuss some of the solutions colleagues of mine have come up with to create the perfectly intonated guitar.