Set neck or Bolt-on neck
- door Guy D'haenens
- •
- 15 aug, 2017
- •
Love it or hate it
The traditional way of attaching a guitar neck to a body of an acoustic guitar is by fitting a precisely cut dove tail tenon into a dovetail mortise that is cut out of the guitar body. The fit should be so precise that almost no glue is needed to hold the two pieces together. This type of guitar neck is called a “set neck”.
As you probably can image from the illustration below, cutting a tenon and a mortise with that precision is not an easy thing to do. It takes years to master. Even with the help of a router, the fit must be hand-tailored to ensure that all the sides of the tenon and mortise are flush and meet with a maximum tolerance of a thousand of an inch. The idea that glue can fill gaps and still hold wood together is an illusion. Glue – even epoxy – works on the principle of (molecular) adhesion and has no strength in itself. The difficult part is that the neck is slightly tilted backwards and the slant of the dovetail of the tenon is not the same as the one of the mortise. It takes a lot of time to get a perfect fit, believe me. But when it’s perfect, the neck is no longer a vibration absorbing piece of wood but a sound transmitter to the body. As it should be.
A less time-consuming way of attaching a guitar neck to a guitar body is by using bolts. There are no difficult dovetail cuts involved here, only a straigth tenon and mortise. And the biggest advantage from my point of view is that the neck can be attached and removed until a perfect fit is achieved. Bolting a neck is by no means an excuse for sloppy work or cutting a tenon that doesn’t fit perfectly into the mortise.
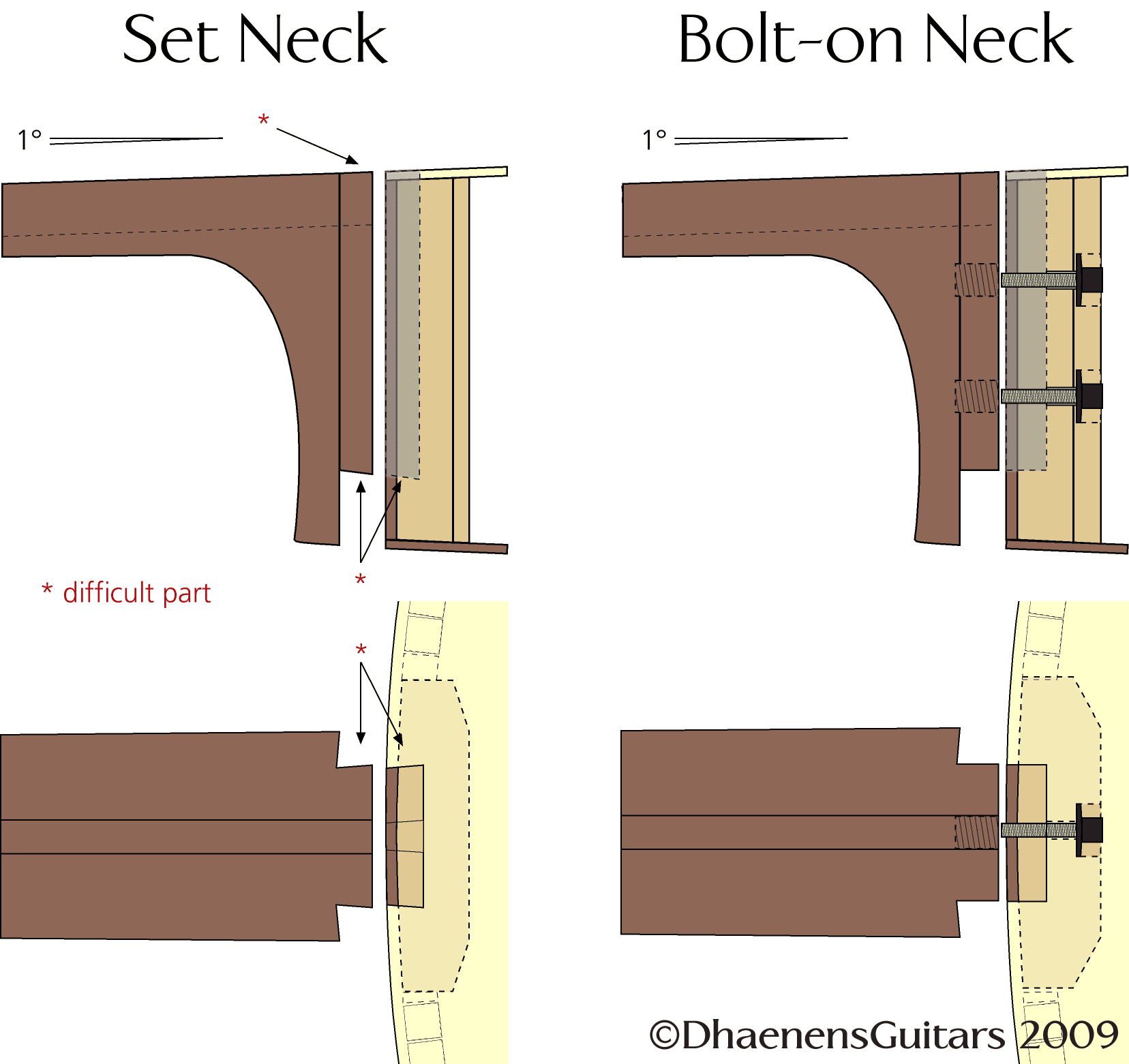
Differences between a set neck and a bolt-on neck
The Taylor Guitar Company started to use bolt-on necks several years ago and they proved that it is a very good way of doing things. Not that it matters much, but it was not Bob Taylor who invented this system; Martin and Howe Orme used it already hundred years ago with far less success and far less precision on some of their guitars. But we owe Bob the credit that he turned an initial bad idea into something great. In fact, bolting necks has now become a standard way of attaching necks.
But Bob didn’t stop there. He also came up with another improvement, an improvement that can hardly be accomplished without the use of CAM: the fingerboard above the 14th fret is supported by an extension of the neck that is also mortised into the top of the guitar without leaving any visual clues. This way, fitting a neck is a breeze because they don’t have to worry about trimming or shimming the end of the fretboard to get it flush with the top of the guitar.
As always, some like bolt-on necks, others hate it.
Those who like it are – generally speaking – young guitar builders and repair persons. They find it easier to cut, easier to fit and above all: it turns a neck reset a less costly event.
Those who dislike or even hate bolt-on necks are – still generally speaking – to be found under older guitar builders who learned the trade the hard way. And they do have a point when they say that a bad neck joint has a deafening effect on tone. But that goes for both set necks and bolt-on necks.
If executed flawlessly, there’s no difference in sound quality between guitars with a set neck or a bolt-on neck. I have used both and I’m quite fond of bolt-on necks. When I’m building a guitar, it takes away the shivers of ruining a perfect neck.
Guy's Blog
Guitars are designed for the 12-tone equal tempered tuning (12-TET). In a 12-tone equal tempered tuning, an octave is divided in 12 semitones at an equidistance of each other: C, C# or Db, D, D# or Eb, E, F, F# or Gb, G, G# or Ab, A, A# or Bb, B.
12-tone equal tempered tuning assumes that e.g. C# is soundwise exactly in the middle of C and D. As you could have guessed, in real life it’s not, it’s only in the mathematical middle and soudwise a bit on the sharp side.
Guitars and all other instruments are tuned at A4= 440 Hz. In 1939 musicians world-wide came to a consensus on that pitch. Before that time, the pitch had been 435 Hz, 374 Hz (1648) and 503 Hz (1361) but those were merely guidelines. Each maestro was free to compose or direct at a lower or higher pitch.
(Hz is the unit to express the number of oscillations of pressure in a sound wave. 440Hz means that there are 440 oscillations per second.)
When you pull an unfretted A-string on a tuned guitar, you’ll hear 110 Hz. When you fret that string at the 12th fret, you’ll hear 220 Hz. That’s exactly the double. Double or half the Hz of any tone is called an octave. Fret that string at the 24th fret and you’ll hear 440 Hz, again one octave higher or 2 octaves higher than the tone of the unfretted string. What you have done each time, is shorten the string by half. A shorter string vibrates at a higher speed thus producing more oscillations per second. A string at 440 Hz oscillates twice as fast as a string of double that length.
The guitar is fretted so we can easily pick the correct notes. Those frets are laid out according to a simple calculation.
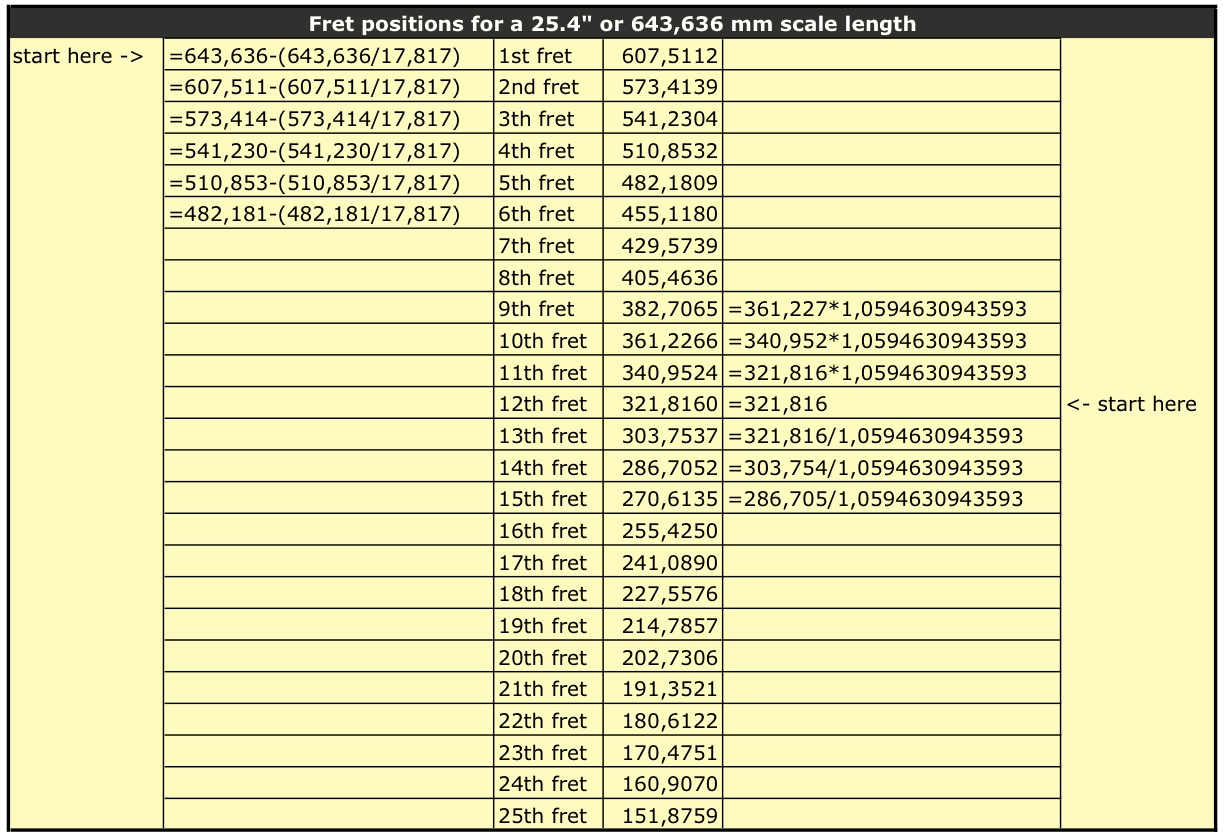
Assume that the scale length of your guitar is 25.4″ (actually it’s 25,34″) or 643,636 mm. The scale length is the distance between the nut and the top of the saddle. The 12th fret will be exactly at 12.7″ (25.4″/2) or 321,818 mm. And since an octave in a 12-TET scale is divided in 12 semitones at equidistance of each other, the math should be fairly simple, no? Alas, dividing 12.7″ by 12 won’t do. That is because we can’t use the distance as input for our calculations, we have to use the frequences. In a 12-TET scale, the ratio of frequencies between two adjacent semitones is the twelfth root of two. And the twelfth root of two is 1.0594630943593.
So starting from the 12th fret, the exact position of the other frets is easily calculated by multiplying or dividing the position of a (previous) fret with 1.0594630943593.
The position of the 11th fret is 340,9543 mm (321,818 * 1,0594630943593); the position of the 10th fret is 361,2626 mm (340,954294100521 * 1,0594630943593); that of the 13th fret is 303,7557 mm (321,818 / 1,0594630943593) and so on.
Another way to determine the fret positions is by using the constant 17.817. The scale length divided by this value gives us the distance from the nut to the first fret.
The following table will make it more clear: