Some thoughts on guitar back and sides woods
- door Guy D'haenens
- •
- 15 aug, 2017
- •
Do we need expensive wood?
Hundred years later, Ovation started creating excellent guitars with fibreglass bodies.
So, if papier-maché and fibreglass are suitable materials for guitar bodies, why does every luthier get excited about the tap tone of some hard-to-get back and sides sets? Is it because they are hard to get, is it because they are expensive or is it because some wood species really add so much depth and 'luminance' to the sound of a guitar?
From experience I can say that the type of wood used does matter: guitars build in a similar way with top plates cut from the same tree, using exactly the same bracing pattern, build simultaneously, will sound different depending on the wood species used for the back and sides. For instance: Mahogany, Rosewood and Monkey Pod have a noticeable longer sustain than Maple, while Mahogany, Monkey Pod and Walnut will produce a warmer sound than Bubinga and Kotibe. But the impact of different species of wood on the sound and on the colour of a guitar is only revealed if the correct construction methods are applied.
Sam Carcagno, a postdoc researcher at the Lancaster University in the UK, is conducting an online listening experiment similar to those of the Leonardo Guitar Research Project folks to determine the extent to which listeners can differentiate steel string guitar back and side wood. You can participate in this listening experiment via http://www.psych.lancs.ac.uk/hearing/the-guitar-experiment/online-tests/.
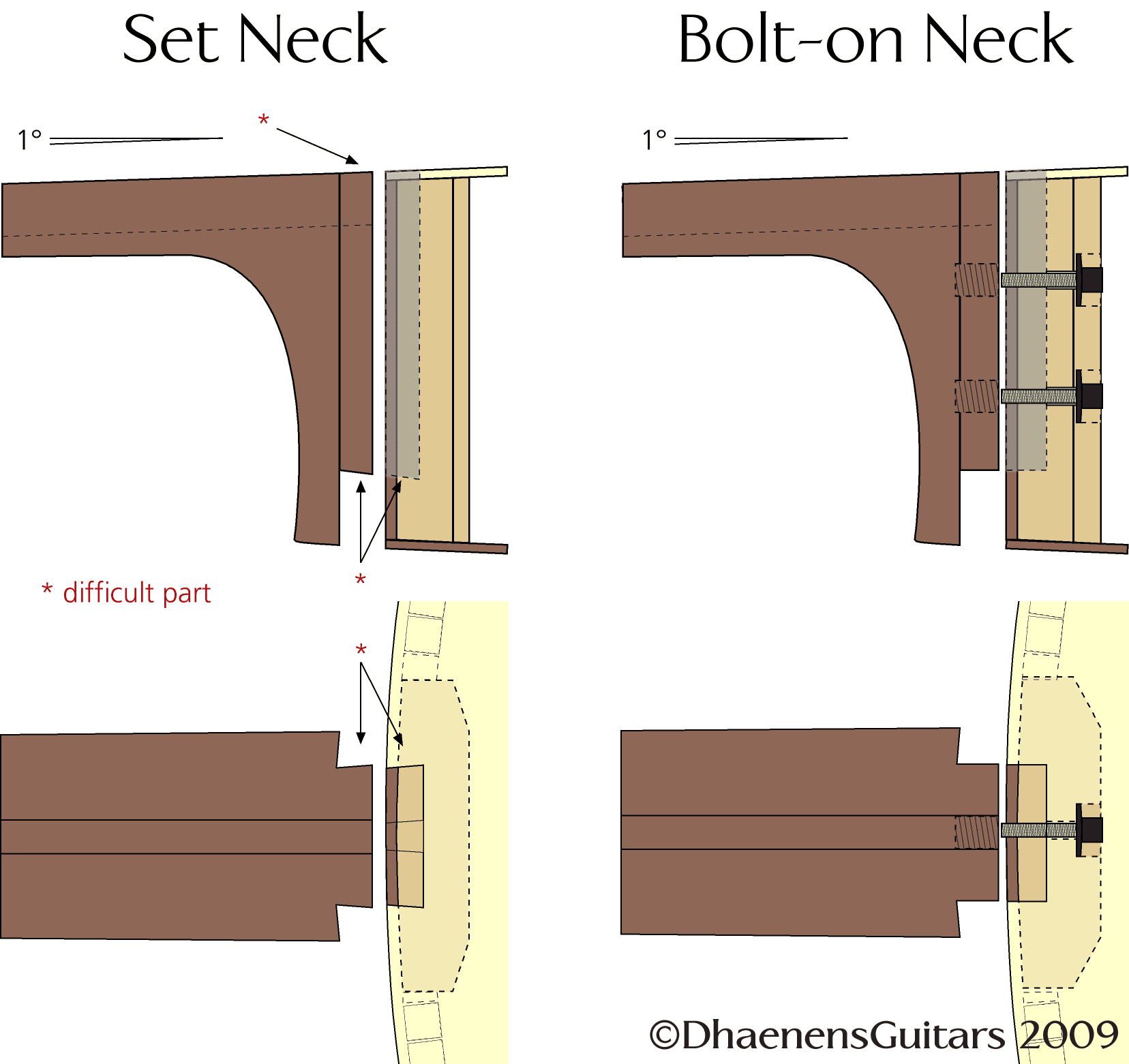
As far as the construction of acoustic guitars is concerned, there are 2 types of backs: reflexive and responsive. Reflexive backs are rather rigid and reflect the sound waves; responsive backs are flexible and act as a second membrane. Ovation guitars with their shell shaped fibreglass bodies are typical or rather obvious examples of guitars with a reflexive back. But there are also many all-wood guitars with reflexive backs; most of them are made of high quality veneer covered plywood. The only way to distinguish the difference in type of back on an all-wood guitar is to pick it up. Guitars with reflexive backs are noticeable heavier due to the thicker back and the heavier bracing.
Building a fine guitar with a reflexive back takes less skill than for one with a responsive back simply because there's only one membrane: the top plate. Responsive backs have 2 membranes and both membranes have to work together to enhance each others frequencies and voice. If they are not in symbiosis, the sound is muffled, the guitar lacks power and luminance and playing such a guitar will be as exciting as tapping on an empty cigar box.
When it comes to choose between a guitar with a reflexive or a responsive back, the only point of consideration is the type of music you want to play on it. A guitar with a reflexive back is very well suited for music styles where a loud and 'less sophisticated' sound is appropriate such as in pop music but it can be used with great results for ragtime and fingerpicking too (Marcel Dadi used many types of Ovations on his recordings and on stage).
Guitars with a responsive back are used whenever a well-balanced and more sensitive sound is required: instrumentals, ballads, singer-songwriters performing solo, unplugged recordings, ...
While guitars with a reflexive back are all more or less in the same price range, prices for guitars with responsive backs can really rock the sky. These price tags not only reflect the qualities of the guitar but also the looks, the exuberance and the scarcity of the sometimes endangered woods. For instance, Brazilian Rosewood, the so called Holy Grail of Guitar Woods, has a price tag of $1000 and up for a back and sides set. In general, figured wood is more expensive because it's hard to find: only 1 to 1000 trees exhibit quilt or any other special figure.
Is this price tag a guarantee for a better guitar? Not really. The choice of wood is important but the dominant factor is the luthier who makes a guitar out of it. The ideal piece of wood, whether it is to be used for a top or for a back, should be quarter sawn. But quarter sawn wood doesn't exhibit lots of figure; extravagant figure is only obtainable in slab sawn or less quarter sawn. So, the heavier the figure, the higher the skills that are needed to create a top instrument.
As I've said before: don't buy a guitar only for its looks unless you can afford a bad bargain. If you want a guitar with a back with lots of figure, don't settle for the first one you see. Luthiers who know how to build an excellent guitar out of highly figured woods do exist.
Guy's Blog
Guitars are designed for the 12-tone equal tempered tuning (12-TET). In a 12-tone equal tempered tuning, an octave is divided in 12 semitones at an equidistance of each other: C, C# or Db, D, D# or Eb, E, F, F# or Gb, G, G# or Ab, A, A# or Bb, B.
12-tone equal tempered tuning assumes that e.g. C# is soundwise exactly in the middle of C and D. As you could have guessed, in real life it’s not, it’s only in the mathematical middle and soudwise a bit on the sharp side.
Guitars and all other instruments are tuned at A4= 440 Hz. In 1939 musicians world-wide came to a consensus on that pitch. Before that time, the pitch had been 435 Hz, 374 Hz (1648) and 503 Hz (1361) but those were merely guidelines. Each maestro was free to compose or direct at a lower or higher pitch.
(Hz is the unit to express the number of oscillations of pressure in a sound wave. 440Hz means that there are 440 oscillations per second.)
When you pull an unfretted A-string on a tuned guitar, you’ll hear 110 Hz. When you fret that string at the 12th fret, you’ll hear 220 Hz. That’s exactly the double. Double or half the Hz of any tone is called an octave. Fret that string at the 24th fret and you’ll hear 440 Hz, again one octave higher or 2 octaves higher than the tone of the unfretted string. What you have done each time, is shorten the string by half. A shorter string vibrates at a higher speed thus producing more oscillations per second. A string at 440 Hz oscillates twice as fast as a string of double that length.
The guitar is fretted so we can easily pick the correct notes. Those frets are laid out according to a simple calculation.
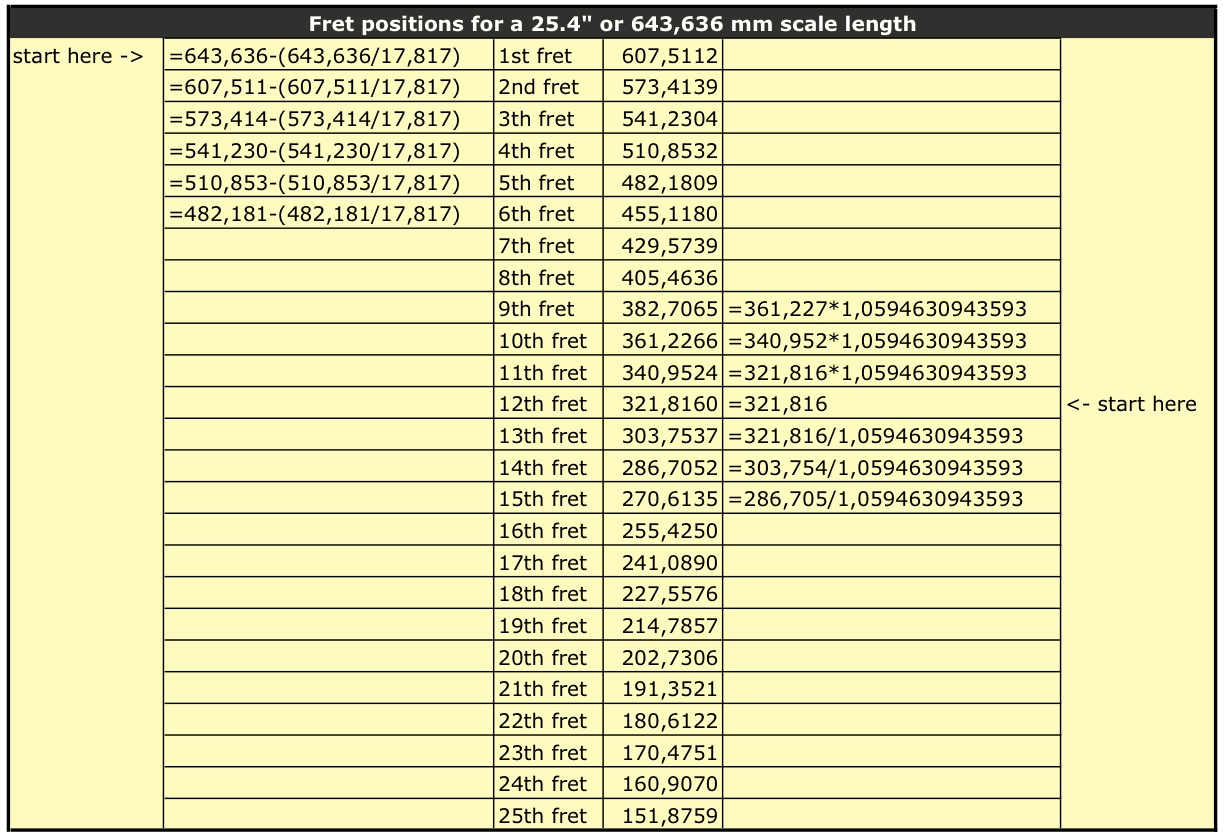
Assume that the scale length of your guitar is 25.4″ (actually it’s 25,34″) or 643,636 mm. The scale length is the distance between the nut and the top of the saddle. The 12th fret will be exactly at 12.7″ (25.4″/2) or 321,818 mm. And since an octave in a 12-TET scale is divided in 12 semitones at equidistance of each other, the math should be fairly simple, no? Alas, dividing 12.7″ by 12 won’t do. That is because we can’t use the distance as input for our calculations, we have to use the frequences. In a 12-TET scale, the ratio of frequencies between two adjacent semitones is the twelfth root of two. And the twelfth root of two is 1.0594630943593.
So starting from the 12th fret, the exact position of the other frets is easily calculated by multiplying or dividing the position of a (previous) fret with 1.0594630943593.
The position of the 11th fret is 340,9543 mm (321,818 * 1,0594630943593); the position of the 10th fret is 361,2626 mm (340,954294100521 * 1,0594630943593); that of the 13th fret is 303,7557 mm (321,818 / 1,0594630943593) and so on.
Another way to determine the fret positions is by using the constant 17.817. The scale length divided by this value gives us the distance from the nut to the first fret.
The following table will make it more clear: